from E/Step Software Inc.
The Right Service At The Right Price: |
Your Competitive Edge John A. Estep, CFPIM, E/Step Software Inc. |
|
When it comes to setting inventory policy, do you guess? Most companies do, but most believe they don't. Typical guesses are 2 weeks' supply or 2 months' supply. Sound familiar? These are called fixed time supplies, and fixed time supplies are guesses. The truth is, you don't have to guess! You can actually know the relationship between inventory policy and customer service. What does that mean? It means you can determine the inventory required to achieve your customer service target. Or, given an inventory budget, you can determine what level of customer service it will buy. If you are currently guessing, then using the right method will give you some valuable benefits: (1) higher customer service, (2) significantly lower inventory (typically a 30% or greater reduction), and (3) less expediting. We will start with a brief Vocabulary Review. Then we will look at three methods for calculating safety stock: Fixed Time Supply, Equal Service, and Optimization. Lastly we discuss alternatives when service requires an inventory which is over budget, looking at the effects of forecast error, service level, lead time, and replenishment frequency. Vocabulary
We will be primarily concerned with Safety Stock, which is stock kept in anticipation of a less-than-perfect forecast. If the forecast error or lead time were zero, there would be no need for safety stock. It is the safety stock which allows you to achieve a particular level of customer service, even though there are errors in the forecast.
The expected stock on hand over time is the sum of the working stock plus safety stock. Though we want to minimize this total (while still achieving our service objectives), we will concentrate in this paper on the safety stock. We do this for two reasons: first, the working stock decision is significantly easier to make and there is much in the literature which covers it adequately; second, for many companies the safety stock makes up the majority of the expected stock on hand. Customer Service Level is the measurement that shows what percentage of the desired stock was delivered to the customer. There are many ways to measure this. For example, if customers order $1,000 worth of product and you were able to ship only $950 of that, that is 95% dollar fill service. If the demand was for 100 cases of product and you shipped 90, that is 90% case fill. If there were 100 line items (i.e., line items on orders from customers) and you could ship 85 of those lines complete, that is 85% line item (or transaction) fill. If the demand came from 10 customer orders and you could fill only 8 of those orders completely, that is 80% order fill. If the total units ordered equaled 200, but you had only 150 units in stock, that is 75% unit fill. If the total weight ordered was 5,000 pounds, but you could ship only 3,000 pounds from stock, that is 60% pound fill. Which of these should you use? Ideally, you want to crawl inside your customers' heads and discover what is most important to them. If your customer has a computerized vendor performance system which measures line item fill, then you want to provide the highest line item fill which is consistent with your inventory budget. In this case you don't have to concern yourself with your case, unit, pound, or order fill rates (unless your customer is monitoring those as well). Two measures of "customer service" don't actually relate to your customer's satisfaction, but do assist you internally in managing your inventory and scheduling your production and/or purchasing. One is called profit fill. If you have customer orders for products which yield $1,000 of profit, but the products you could ship from stock yielded only $700 of profit, then that is 70% profit fill. Maximizing your profit fill means you will get the highest profit possible from any given inventory level. Of course, if you shorted your customer on a critical part, he's not going to care that it was the least profitable part for you of all the things he ordered. Finally, let's consider lot fill. Suppose you have 1,000 manufactured or purchased lots being delivered to stock each year. If 900 of those lots arrive while there is still stock on the shelf (the other 100 arrive after you have run out) that is 90% lot fill. What good is that? Think of it from an expediting pressure point of view. Ninety percent of the time, there will be no panicked telephone calls asking you to expedite the particular lot. On 10% of lots you may get phone calls. If you can expedite the lots (i.e., get them in in less than normal lead time) you could provide 100% service (by any measure) while only paying for the inventory required to achieve 90% lot fill. As you will see below, the inventory otherwise required to boost service from 90% to 100% can be huge, so a little expediting can go a long way to reducing your inventory. Three Methods for Setting Inventory Targets We will look at three ways to do this: (1) Fixed Time Supply guess, (2) Equal Service, and (3) Optimization. Only the latter two actually work; i.e., they compute the inventory you need to meet your service target. The fixed time supply method is actually a guess and the resulting service and inventory are only incidental to the process. It is a great way to achieve low service with high inventory, if that is your goal! Method 1: Fixed Time Supply Guess
Simply stated, the problem is to determine how much safety stock is required to achieve a desired level of customer service. Starting with an example so simple that we can work without a computer, consider the situation in Figure 1, which has information on a two-item product line. Since each part costs $1.00, we can work with dollars or units interchangeably. Suppose you want to know how much safety stock is required to give 95% customer service. Most companies, when faced with this question, handle the situation by educated guessing. If service is too low, say 90%, and finished goods safety stock last year averaged six weeks, they may decide to increase it this year to perhaps two months. In reality, there is not enough information provided about this product line to make any decision. Let's provide some additional information and see if we can do better. (See Figure 2.)
Now parts A and B no longer look identical in all respects—in fact their forecasts are very different. The forecast for part A, with 95% confidence, is between 1,800 and 2,200 pieces per month. B's forecast, with the same confidence, is between net returns of 4,000 (zero if returns are not possible) and 8,000, but with a most likely value of 2,000. Clearly, different measures are justified for the two parts! In fact, since the given forecast confidence interval just happens to match our desired service level, the correct safety stock is simply the same value as the confidence limit. (See Figure 3.)
This safety stock achieves your objective of 95% customer service, but at a cost of almost 25% less than the two month safety stock. What happened to customer service in the meantime? Consider the two parts individually.
For part A, the two-month supply is 20 times more than necessary. So the service is something higher than 95% (most likely 100%) and now drops to exactly 95%. For part B, the two-month supply is only two-thirds enough to reach 95% customer service. The information provided is insufficient to tell precisely, but it is safe to assume that service was substantially below 95%; we'll estimate it at 60%. This means aggregate service was only 80%. So you have a choice of 80% service at a cost of $8,000, or 95% service (the target) for $6,200. Tough decision! Fixed Time Supply Guesses Do Not Work One concludes two things from this: (1) it is indeed possible to raise service at the same time you reduce inventory; and (2) fixed time supply guesses do not work. You pay too much in inventory for service that falls short of your objectives. Safety stock, whose purpose is to cover errors in the forecast, must be set according to the size of the errors—not according to the size of the forecast. Why do most companies use fixed time supply guesses? Because they are easier to understand and easier to compute. Unfortunately they do not do the job. The reason this works with such dramatic result is that most forecast errors are distributed according to the normal error distribution. In layman's terms, this means there are usually a large number of small errors and a small number of large errors. Setting safety stocks using a fixed time supply results in too much inventory for most items (the ones with the small errors) and too little inventory for a few items (the ones with the large errors). The Need For A Computer Most of us have far more than just two products, and management never seems content with a single level of customer service. When told that 95% service can be obtained for $6,200, the response is frequently either "How much would 97% cost?" or "How much service could I get for $5,500?" For answers to both of these questions, or when you have many products, you need to get a computer involved. A computer, using the methods described in Reference 1, can evaluate any customer service level for any number of products. The Sample To Be Analyzed To keep things relatively simple, we'll look at a sample of four parts drawn from an actual service parts environment, which is the most difficult application from a forecast accuracy point of view. The demand and forecast errors are real. The four parts have an annual volume in excess of $20 million. Current customer service is 96.4% dollar fill, while our service target is 98% dollar fill. Safety stock to achieve this service has been set initially to a 52-day fixed time supply guess, or just over $4 million. Working stock for these parts has been set initially to a half month supply; i.e., all four parts are replenished once per month.
For most of our work we will let the computer evaluate the formulas for each individual part, but only display the aggregate values across all the parts. Initial details for the parts are shown in Figure 4. While inventory is a constant 52 days for each part, service varies wildly from far above our 98% target for 3 parts and only 60% for one part. Calling the aggregate service 96.4% hides multiple sins here. It's like the fellow with his feet frozen in a block of ice and his head in a hot oven—on the average he's at room temperature, but comfortable? No. Evaluate Using Fixed Time Supply Since we started with Fixed Time Supply, let's use this method to examine the service available when inventory varies from 20 to 90 days.
Here we see that 20 days' supply buys 86.9% aggregate dollar fill, while 90 days' supply buys 98.8%. Let's look at 98.0% (our target) which with this method costs $5.8 million in inventory. While the service is 98% in the aggregate, the details show a very different picture.
While the inventory is a constant 74 days' supply, the service is either wonderful or awful, but the aggregate is 98%. Since our aim is consistent service, not consistent days of inventory, we need to do something different. The Shape of the Curve
There are three measures of service graphed above, but the green curve is the dollar fill measure we have been examining. Notice that as service approaches 100% the cost to achieve it increases exponentially, while as service drops below 90% the cost flattens out. Notice also that the current position (marked by the green circle) shows the service and inventory intersecting exactly on the curve. This is to be expected as we used a 52 day fixed time supply guess to compute the initial inventory levels. This example illustrates one of the principles of setting finished goods safety stock: more service is more and more expensive. For example at the low-service end of Figure 5, increasing safety stock by $0.4 million from $1.6 million to $2.0 million buys an increase in service of 3.2 points, from 86.9 to 90.1. Yet at the other end, increasing safety stock by $0.4 million from $6.6 million to $7.0 million buys only an additional 0.2% service (98.6 to 98.8). At the high end of the service range, very small changes in service are accompanied by very large swings in requisite safety stock. At the low end, very small changes in safety stock cause very large swings in customer service. In practice, there are a couple of ways you can make this work for you. If you need high service, say 98 to 99%, but either will suffice, setting service at 98% rather than 99% can save you a substantial percentage of your safety stock. On the other end of the service spectrum, if you have a product line for which you feel you can only afford 85% service, you may find a very small percentage increase in safety stock is required to give you 90% service or more—a change that customers are far more likely to notice. Method 2: Equal Service Method In Figure 6, the 98% aggregate service—while arguably better than the aggregate 96.4% we started with—varies wildly. What we want is service that is consistently at the 98% target for every part. The method which does that for us is called the Equal Service method. Let's look at a service range from about 86% to 99.9% dollar fill.
While this method does, in fact, insure that all parts in the group get equal service, it also sets the inventory targets based on the error in the forecast, not the size of the forecast. The efficiency gained is astounding. Notice, for example, that 99.9% service costs just $4.8 million in inventory here, while using the fixed time supply method it required over $7 million to achieve 98.8%. If we graph the service/inventory tradeoff curve we see something quite interesting. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
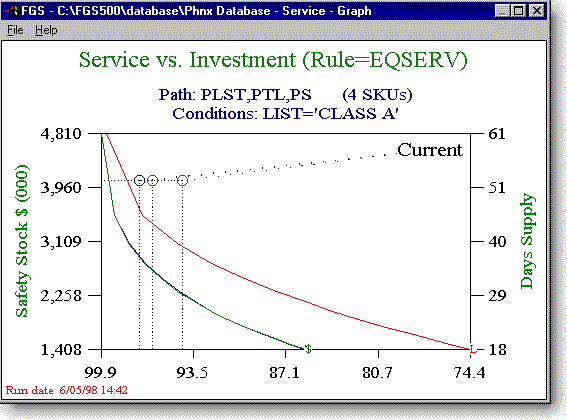 In contrast with Figure 7, now the curve (in this case the Equal Service curve) is out
in front of the current position. This means that instead of the current 52 day fixed time
supply, we have the option of moving left to the curve (keeping total inventory constant
while improving service), moving down to the curve (keeping aggregate service the same
while reducing inventory) or moving diagonally left and down (cutting inventory while
raising service). The latter option is the preferred one. The reason for this is that no
matter what your service and inventory targets, every company must first demonstrate to
top management that it can control service and inventory. The best way to do this is to
reduce inventory at the same time you improve service. Once you have demonstrated your
credibility on this issue then you can implement your ultimate targets.
In contrast with Figure 7, now the curve (in this case the Equal Service curve) is out
in front of the current position. This means that instead of the current 52 day fixed time
supply, we have the option of moving left to the curve (keeping total inventory constant
while improving service), moving down to the curve (keeping aggregate service the same
while reducing inventory) or moving diagonally left and down (cutting inventory while
raising service). The latter option is the preferred one. The reason for this is that no
matter what your service and inventory targets, every company must first demonstrate to
top management that it can control service and inventory. The best way to do this is to
reduce inventory at the same time you improve service. Once you have demonstrated your
credibility on this issue then you can implement your ultimate targets.
Let's look at the details by part for our 98% service target.
Part |
Safety Stock in Units |
Safety Stock in $Std Cost |
Safety Stock in Days |
$ Fill Service |
A |
175 |
1,675,231 |
32.1 |
98.0 |
B |
776 |
998,122 |
142.1 |
98.0 |
C |
460 |
151,337 |
15.3 |
98.0 |
D |
1,089 |
268,544 |
29.1 |
98.0 |
Total |
$ 3,093,234 |
39.5 |
98.0 |
|
| Figure 10: 98% Dollar Fill Using the Equal Service Method | ||||
Now this is 98% service! We have consistent 98% dollar fill service for every part in the service group; and, because we are computing targets based on the forecast error, the inventory required to achieve 98% is only $3.1 million, a drop of 25% from the current $4 million required to achieve only 96.4% aggregate—but which varies wildly from that aggregate at the detailed level. Here the variation is in the days of inventory required to achieve the 98% target.
Method 3: Optimized Safety Stock
Now that we have eliminated variation in individual service levels, let's consider whether we might allow a little variation. If we do so, perhaps we could increase service slightly for products with small forecast errors in order that we might decrease service slightly for products with large errors. We will constrain the solution, however, to require that the aggregate service still meet our target. At 98% for example there is less room above the target than below. This means that we will have to increase service on more items than we decrease. The solution to this problem is called optimization. While there are an infinite number of combinations that achieve the aggregate service target, only one solution has the lowest possible inventory. Optimization is the name of the technique which finds this optimum solution. Let's begin by looking at the high end of the service range, shown in Figure 11.
----------Investment---------- |
----------Service---------- |
||||
(Safety Stock) |
$ Value |
Percent |
|||
Dollars |
Weeks |
Days |
Backorders |
$ Fill |
|
| Projected: | 2,461,542 |
6.3 |
31 |
815,006 |
96.0 |
2,875,261 |
7.3 |
37 |
482,209 |
97.6 |
|
3,267,409 |
8.3 |
42 |
281,650 |
98.6 |
|
3,626,081 |
9.3 |
46 |
166,092 |
99.2 |
|
3,941,030 |
10.1 |
50 |
101,391 |
99.5 |
|
4,210,870 |
10.8 |
54 |
64,945 |
99.7 |
|
4,444,183 |
11.4 |
57 |
43,456 |
99.8 |
|
4,656,435 |
11.9 |
59 |
29,763 |
99.9 |
|
4,865,535 |
12.4 |
62 |
20,267 |
99.9 |
|
5,087,402 |
13.0 |
65 |
13,327 |
99.9 |
|
5,331,674 |
13.6 |
68 |
8,295 |
100.0 |
|
5,598,087 |
14.3 |
72 |
4,873 |
100.0 |
|
5,875,407 |
15.0 |
75 |
2,748 |
100.0 |
|
6,144,888 |
15.7 |
78 |
1,537 |
100.0 |
|
| Current: | 4,070,942 |
10.4 |
52 |
739,800 |
96.4 |
| Figure 11: Optimized Dollar Fill Rule From 96% to 99.99% | |||||
This shows us a range of service from 96% to 100% (actually 99.99%) along with the requisite safety stock in aggregate dollars and as an average (not fixed) time supply. This analysis indicates what is possible to achieve by optimizing dollar fill and is in stark contrast to the current 52-day fixed time supply. For example, if we are willing to drop service from the current 96.4% to 96%, the corresponding safety stock drops almost 40% from about $4 million to about $2.5 million. Conversely if we need 100% service for this group, the cost in inventory is somewhere between $5.5 million and $6.5 million, depending on how precisely you want to hit the target ($6.5 million buys 99.99%, the others a bit less).
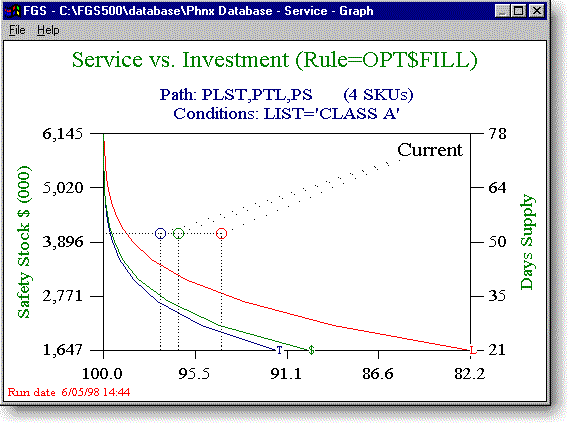 |
Let's look at the service/inventory curve for this scenario.
Comparing this with the Equal Service curve in Figure 9, you see that the curve is even further to the left of the current position. This means that with optimization you can do even better than with equal service.
You can approach inventory planning from two points of view. One is to say, "I have a fixed amount available for safety stock; how much service can I afford?" The other is to specify the service and find out what it costs in inventory. What you are doing, essentially, is determining the price list for service. We will look at the situation from both points of view.
Working From A Fixed Budget
Assume you have a safety stock budget of $3.5 million for this product line. Looking up this figure in column one of Figure 11, you find it falls between $3.3 and $3.6 million. The corresponding service falls between 98.6 and 99.2%. You want to know service more precisely, however, so do an analysis on this service range to home in on the correct value.
----------Investment---------- |
----------Service---------- |
||||
(Safety Stock) |
$ Value |
Percent |
|||
Dollars |
Weeks |
Days |
Backorders |
$ Fill |
|
| Projected: | 3,259,361 |
8.3 |
42 |
284,892 |
98.6 |
3,290,450 |
8.4 |
42 |
272,544 |
98.7 |
|
3,321,305 |
8.5 |
42 |
260,751 |
98.7 |
|
3,351,917 |
8.6 |
43 |
249,491 |
98.8 |
|
3,382,280 |
8.6 |
43 |
238,743 |
98.8 |
|
3,412,387 |
8.7 |
44 |
228,485 |
98.9 |
|
3,442,230 |
8.8 |
44 |
218,699 |
98.9 |
|
3,471,803 |
8.9 |
44 |
209,363 |
99.0 |
|
3,501,100 |
8.9 |
45 |
200,460 |
99.0 |
|
3,530,115 |
9.0 |
45 |
191,971 |
99.1 |
|
3,558,843 |
9.1 |
45 |
183,877 |
99.1 |
|
3,587,278 |
9.2 |
46 |
176,162 |
99.1 |
|
3,615,416 |
9.2 |
46 |
168,808 |
99.2 |
|
3,643,253 |
9.3 |
47 |
161,800 |
99.2 |
|
| Current: | 4,070,942 |
10.4 |
52 |
739,800 |
96.4 |
| Figure 13: Optimized Dollar Fill Rule From 98.6% to 99.2% | |||||
From the analysis in Figure 13 you see that your budget falls between the $3.471 and $3.5011 million lines. Since the corresponding service for both is 99.0, we can conclude that a safety stock budget of $3.5 million for this product line will buy us 99% customer service. This is a savings of $0.5 million from the current fixed time supply while still increasing service from 96.4% to 99%.
Working From A Fixed Service Target
Using the same type of repetitive search (here done for us by the computer) you can start with a particular service target and observe the required safety stock. For example, assume you need to achieve 98% for this product line.
----------Investment---------- |
----------Service---------- |
||||
(Safety Stock) |
$ Value |
Percent |
|||
Dollars |
Weeks |
Days |
Backorders |
$ Fill |
|
| Projected: | 3,003,075 |
7.7 |
38 |
406,483 |
98.0 |
3,042,413 |
7.8 |
39 |
385,335 |
98.1 |
|
3,081,498 |
7.9 |
39 |
365,266 |
98.2 |
|
3,120,316 |
8.0 |
40 |
346,231 |
98.3 |
|
3,158,854 |
8.1 |
40 |
328,185 |
98.4 |
|
3,197,099 |
8.2 |
41 |
311,084 |
98.5 |
|
3,235,037 |
8.3 |
41 |
294,888 |
98.6 |
|
3,272,655 |
8.4 |
42 |
279,554 |
98.6 |
|
3,309,939 |
8.5 |
42 |
265,042 |
98.7 |
|
3,346,876 |
8.6 |
43 |
251,316 |
98.8 |
|
3,383,452 |
8.6 |
43 |
238,336 |
98.8 |
|
3,419,657 |
8.7 |
44 |
226,066 |
98.9 |
|
3,455,478 |
8.8 |
44 |
214,473 |
98.9 |
|
3,490,903 |
8.9 |
45 |
203,521 |
99.0 |
|
| Current: | 4,070,942 |
10.4 |
52 |
739,800 |
96.4 |
| Figure 14: Optimized Dollar Fill Rule From 98% to 99% | |||||
Setting service to 98% (up from 96.4%) requires just over $3 million in safety stock, a savings of over $1 million, or about 25%. Let's look at the details for our 98% target:
Part |
Safety Stock in Units |
Safety Stock in $ Std Cost |
Safety Stock in Days |
$ Fill Service |
A |
180 |
1,728,195 |
33.1 |
98.3 |
B |
625 |
803,181 |
114.4 |
94.1 |
C |
572 |
188,356 |
19.0 |
99.0 |
D |
1,149 |
283,343 |
30.7 |
98.4 |
Total |
$ 3,003,075 |
38.4 |
98.0 |
|
| Figure 15: 98% Optimized Dollar Fill Details | ||||
As you can see, we have reintroduced some small service variations, although nothing like what we started with. Service on three parts is slightly higher, but none higher than 99%. Service on one item has dropped to 94.1% (but not to 60%). It is no coincidence that this item also has the highest inventory in days. Item B has a large forecast error relative to the others. This serves as further proof that fixed time supply is not the method to use. Safety stock has dropped for parts A, C, and D; by about 75% for part C. It has increased by over 50% for part B. Part B with a 114-day safety stock can support just 94% service, while part C with a 19-day supply can expect 99% customer service!
Which Method Should You Use?Let's put all three methods up for comparison. From the service point of view, here's how they compare.
| Method | Minimum Service % |
Maximum Service % |
Aggregate $ Fill Service % |
| 1. Fixed Time Supply Guess | 78.1 |
100.0 |
98.0 |
| 2. Equal Service | 98.0 |
98.0 |
98.0 |
| 3. Optimized $ Fill | 94.1 |
99.0 |
98.0 |
| Figure 16: Service Comparison | |||
Under the fixed time supply method, service is essentially out of control. The only possibilities to consider are the other two: equal service if you must have 98% on everything, or optimization if you can allow a slight variation. From an inventory point of view, however, the differences are even more striking:
| Method | Average Inventory in Days |
Total Safety Stock $ |
Inventory Savings over Fixed Time Supply |
| 1. Fixed Time Supply Guess | 74.0 |
5,781,219 |
0.0 % |
| 2. Equal Service | 39.5 |
3,093,234 |
46.5 % |
| 3. Optimized $ Fill | 38.4 |
3,003,075 |
48.1 % |
| Figure 17: Inventory Comparison | |||
Either method 2 or 3 is a significant improvement over fixed time supply. In this case optimization shows about a three percent improvement over equal service. Sometimes, however, the difference is substantially more. A client using optimization was once asked by an overseas affiliate what he thought of their plan to use a less capable package. His immediate reaction was that they would give up the benefits of using selectable forecast calendars (see Reference 2) and optimization. (Since this was a service parts application, the first was a significant blow to forecast accuracy.) The affiliate expressed doubt that something as nebulous sounding as "optimization" could have any substantial impact. The client, intrigued, said "Let's find out." Stepping over to his computer, he noted the service level being achieved by their current optimization and then ran an analysis of what it would cost to achieve that same service level without optimization (using the equal service rule). The inventory went up fifty percent!
Other Forms of Optimization
There are many forms of optimization. Each achieves the target service level for the chosen measure of service while minimizing the inventory required to do so. Or, from the other point of view, for a given inventory investment each maximizes the service obtained for the chosen measure. The above dollar fill optimization provides the highest dollar fill service (i.e., minimizes the dollars short) for any given inventory level. Other optimizations minimize the number of customer line items short, the number of units short, cases short, pounds short, etc. One can even optimize on profit fill, achieving the highest profit dollars possible from any given inventory level. Of course, your customers are not likely to want to hear that the reason you are out of a needed part is that you make little profit on it.
There is one other optimization which—while it is not directly related to customer service—can make your life easier. It is called Optimized Lot Fill. This method minimizes the number of production lots (manufactured or purchased) which will arrive after you have run out of stock. That, in turn, minimizes expediting. If you do expedite, this means you could set an inventory which achieves, say, 95% optimized lot fill. Then if you can successfully expedite the remaining 5% of your replenishment lots, this means you can achieve 100% service, while only paying for 95% with inventory, plus expediting 5%. For many companies that is a real bargain. You can literally trade the cost of inventory against the cost of expediting to achieve your objectives.
Options To Consider When Over Budget
Going back to the 98% service level using optimized safety stock, what should you do if the $3 million is too high, yet 98% is still the target? First, consider that there are several things which affect safety stock. These are (1) forecast error, (2) service level, (3) lead time, and (4) working stock (or replenishment frequency). Except for forecast error, there are penalties associated with tweaking any of these in order to reduce the safety stock. The penalties may or may not exceed the benefits in reduced safety stock. Let's consider each of these areas.
Forecast Error
Of the four areas, this is the one that is (almost) free. A reduction in the forecast error yields a linear reduction in safety stock to achieve any given level of service. This means a 25% reduction in forecast error yields a 25% reduction in safety stock. The only penalty associated with attacking forecast error is the time you invest in doing so.
In our example, you could look over the four parts and choose a likely candidate to work on. Part A seems a good choice since it has a safety stock (in dollars) more than twice as great as any of the others. Part B may be a better choice, however, since its safety stock is almost 3.5 times greater than part A when expressed as a time supply. This is the same as thinking of the safety stock as a percentage of the forecast, and in B's case it is for service substantially lower than A's.
You might want to check with the sales people or product managers to find out whether unusual events are affecting the ability to forecast this part. It may be that there are people with information which the computer does not have. This is called gathering marketing intelligence.
Another approach to reducing forecast error is to consider whether you are trying to forecast part B too frequently. You may find that by forecasting the part less frequently than monthly—quarterly or semiannually, for example—you can substantially reduce the forecast error.
Recently a consultant, in a column in a major trade publication, expressed the opinion that all companies should forecast all of their parts monthly. His reasoning was that weekly forecasting was too often for some companies and quarterly forecasting was too infrequent for others. This is rather like saying that since size 6 shoes are too small for some people, and size 10 shoes are too large for others, everybody ought to wear a size 8!
A more enlightened approach is to forecast each item on the calendar most appropriate for that item. In the fast food business this can mean forecasting weekly, biweekly, and in some cases, daily. For the service parts environment it means forecasting bimonthly, quarterly, semiannually, and even annually. One company doing this achieved a 43% reduction in their workload at the same time they achieved 30% lower aggregate forecast errors (and inventory)! This method is discussed further in References 2 and 4.
Service Level
While we said we wanted to maintain a 98% service level, you might take this opportunity to re-examine your service categories. This might indeed be a category which requires 98%, but you ought to consider whether part B belongs in this service category. If, after gathering information and talking with the right people, you decide that part B can be assigned to a different (i.e., lower) service group, you will find the total safety stock requirement to be less. Even using optimization, the service for the remaining parts can drop closer to the 98% target now that they no longer have to compensate for the huge error in part B, thus reducing their safety stock. If B is set to 94.1% or anything lower, the safety stock for it will also be reduced.
Service category considerations depend greatly on the type of business. Some of the things to consider are how the customer uses the product (critical vs. non-critical) and the consequences of running out, competition, ingredients, manufacturing processes, suppliers, etc. You may find that the typical ABC classification scheme bears little relevance to the establishment of service classes.
Lead Time
The longer lead time for a part, the greater its safety stock, because it must protect the forecast over a longer period of time. This is not a linear, but rather a square root relationship. This means that reducing the lead time by a factor of four (75%) reduces the safety stock by a factor of two (50%). This is a good area to consider if you have unrealistically inflated lead times on file. You want the lead times in the computations to reflect reality as closely as possible.
If your lead times are realistic and accurate, then reducing them is likely to be associated with increasing the cost of the product. For example you might require your suppliers to keep larger stocks so you (and they) will be able to respond more quickly. Most likely they will want to be paid for this privilege. In fact, you might consider doing just the opposite. You could find that freezing the schedule for a longer period results in such additional efficiencies that your costs drop more than your safety stocks increase. (Perhaps we should add cost review to the above list.)
An alternative to having your vendors maintain your inventory is to keep an inventory yourself in raw materials or components (also known as semi-finished). Recent developments in technology have made it possible—just as you can compute finished goods safety stocks—to compute component safety stocks. Where components or intermediates have long lead or processing times, and where there is some amount of commonality of components, this technique can lead to significant (i.e., 30% or more) reductions in total inventory (finished plus component plus raw material). For more information on this, contact the author.
If you do address lead time, use Pareto analysis to decide where to spend your time. One service parts company did such an analysis on what their inventory savings would be if they could cut their lead times. They were startled to discover that by cutting lead times on only 13% of their parts, they could achieve 80% of the total inventory savings they would achieve if they cut lead times on all their parts. Any time you can get 80% of the pay back while doing only 13% of the work, you know you're on the right track! The trick, of course, is to pick the right 13%.
Working Stock/Replenishment Frequency
The level of working stock also affects the safety stock. This is perhaps easier seen when thinking of working stock as replenishment frequency. If a product is replenished only once per year, it is less likely to be out of stock than one which is replenished weekly. The one has, on the average, only one opportunity per year to run out, while the other has 52. Normally the best approach is to use the appropriate Economic Order Quantity (EOQ) formula to compute the working stock before computing the safety stock. If you have a situation with unusually large forecast errors, you may want to set a replenishment quantity higher than the EOQ. In this case the increased working stock is more than offset by the reduction in safety stock. Methods for both situations are discussed in Reference 1.
Summary
There is a well-defined relationship between customer service and finished goods inventory, but it is dependent on the forecast accuracy, service level, and replenishment frequency to a much greater extent than it is on the forecast size. Using techniques well-documented in the literature, it is possible to develop a price list for service, but without having to guess. Doing so puts the inventory where it is required, matching service to management's objectives. By examining forecast error, service categories, lead times, and replenishment frequencies you can manage the inventory to the point that the minimum possible inventory is used to meet your service objectives.
The benefits from doing so are (1) significantly lower inventory (e.g., 30% or more), (2) higher customer service, (3) reduced expediting, and (4) no sleepless nights worrying about whether a fixed time supply guess is sufficient.
References| 1. Greene (ed.), Production and Inventory Control Handbook, APICS, 1970, Chapter 19; or Production and Inventory Control Handbook (2nd ed.), APICS, 1987, Chapter 29. | |
| 2. Estep, J., "A Simple Technique For Reducing Forecast Errors," APICS 30th Annual International Conference Proceedings, APICS, 1987, pp. 291-293. | |
| 3. Applications section, IIE Solutions, Institute of Industrial Engineers, July, 1997. | |
| 4. Beck, J., "SPC and Selectable Forecast Calendars Work Magic for GE Aircraft Engines' Service Parts Operation," APICS 38th Annual International Conference Proceedings, APICS, 1995, pp. 477-481. |
About the Author
John A. Estep, an APICS Fellow, is president of E/Step Software Inc., a Yakima, Washington based company specializing in systems for finished goods/service parts forecasting and inventory planning. With a background in mathematics, operations research, and computer engineering, he worked on his first forecasting system for an apparel manufacturer in 1970, and has since counseled hundreds of companies on their forecasting needs.
| For more information, call: |
| E/Step Software Inc. |
| 12015 Summitview Road, Yakima, WA 98908 , USA |
| Tel. (509) 853-5000 |
| Fax (509) 853-5002 |
| Email: |
| Web site: www.EstepSoftware.com |